Stoer-Wagner 算法

定义

由于取消了 源汇点 的定义，我们需要对 割 的概念进行重定义。

（其实是网络流部分有关割的定义与维基百科不符，只是由于一般接触到的割都是「有源汇的最小割问题」，因此这个概念也就约定俗成了。）

割

去掉其中所有边能使一张网络流图不再连通（即分成两个子图）的边集称为图的割。

即：在无向图 中，设 为图 中一些弧的集合，若从 中删去 中的所有弧能使图 不是连通图，称 图 的一个割。

有源汇点的最小割问题

同

最小割 中的定义。

无源汇点的最小割问题

包含的弧的权和最小的割。也称为全局最小割。

显然，直接跑网络流的复杂度是行不通的。

---

Stoer-Wagner 算法

引入

Stoer-Wagner 算法在 1995 年由Mechthild Stoer与Frank Wagner提出，是一种通过 递归 的方式来解决 无向正权图 上的全局最小割问题的算法。

性质

算法复杂度 一般可近似看作 。

它的实现基于以下基本事实：设图 中有任意两点 。那么任意一个图 的割 ，或者有 在同一连通块中，或者有 是一个 割。

过程

1. 在图 中任意指定两点 ，并且以这两点作为源汇点求出图 的 最小割（定义为cut of phase），更新当前答案。
2. 「合并」点 ，如果图 中 大于 ，则回到第一步。
3. 输出所有cut of phase的最小值。

合并两点 ：删除 之间的连边 ，对于 中任意一点 ，删除 ，并将其边权 加到 上

解释：如果 在同一连通块，对于 中的一点 ，假如 ，那么 也一定成立，否则因为 连通， 连通，导致 在同一连通块，此时 将比 更优。反之亦然。所以 可以看作同一点。

步骤 1 考虑了 不在同一连通块的情形，步骤 2 考虑了剩余的情况。由于每次执行步骤 2 都会使 减小 ，因此算法将在进行 后结束。

S-T 最小割的求法

（显然不是网络流。）

假设进行若干次合并以后，当前图 ，执行步骤 1。

我们构造一个集合 ，初始时令 。

我们每次将 中所有点中，满足 ，且权值函数 最大的节点加入集合 ，直到 。

其中权值函数的定义：

（若 ，则 ）。

容易知道所有点加入 的顺序是固定的，令 表示第 个加入 的点，； 表示 被加入 后 的大小，即 被加入的顺序。

则对任意点 ，一个 到 的割即为 。

证明

定义一个点 被激活，当且仅当 在加入 中时，发现在 此时最后一个点 早于 加入集合，并且在图 中， 与 不在同一连通块。

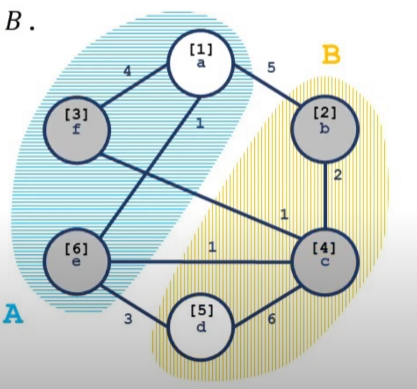
如图，蓝色区域和黄色区域为两个不同的连通块，方括号中的数字为加入 的顺序。灰色节点为活跃节点，白色节点则不是活跃节点。

定义 ，也就是严格早于 加入 的点，令 为 的诱导子图（点集为 ）的边集。（注意包含点 。）

定义诱导割 为 。。

由于 ，并且 不在同一连通块，因此 会被激活，由此可以得出 。

---

复杂度分析与优化

contract操作的复杂度为 。

一共进行 次contract，总复杂度为 。

根据

最短路 的经验，算法瓶颈在于找到权值最大的点。

在一次contract中需要找 次堆顶，并递增地修改 次权值。

斐波那契堆 可以胜任 查找堆顶和 递增修改权值的工作，理论复杂度可以达到 ，但是由于斐波那契堆常数过大，码量高，实际应用价值偏低。

（实际测试中开 O2 还要卡评测波动才能过。）