Prufer 序列

本文翻译自 e-maxx Prufer Code。另外解释一下，原文的结点是从 开始标号的，本文我按照大多数人的习惯改成了从 标号。

这篇文章介绍 Prufer 序列 (Prufer code)，这是一种将带标号的树用一个唯一的整数序列表示的方法。

使用 Prufer 序列可以证明凯莱定理 (Cayley's formula)。并且我们也会讲解如何计算在一个图中加边使图连通的方案数。

注意：我们不考虑含有 个结点的树。

Prufer 序列

引入

Prufer 序列可以将一个带标号 个结点的树用 中的 个整数表示。你也可以把它理解为完全图的生成树与数列之间的双射。

显然你不会想不开拿这玩意儿去维护树结构。这玩意儿常用组合计数问题上。

Heinz Prufer 于 1918 年发明这个序列来证明凯莱定理。

对树建立 Prufer 序列

Prufer 是这样建立的：每次选择一个编号最小的叶结点并删掉它，然后在序列中记录下它连接到的那个结点。重复 次后就只剩下两个结点，算法结束。

显然使用堆可以做到 的复杂度

```cpp
// 代码摘自原文，结点是从 0 标号的
vector<vector<int>> adj;

vector<int> pruefer_code() {
  int n = adj.size();
  set<int> leafs;
  vector<int> degree(n);
  vector<bool> killed(n, false);
  for (int i = 0; i < n; i++) {
    degree[i] = adj[i].size();
    if (degree[i] == 1) leafs.insert(i);
  }

  vector<int> code(n - 2);
  for (int i = 0; i < n - 2; i++) {
    int leaf = *leafs.begin();
    leafs.erase(leafs.begin());
    killed[leaf] = true;
    int v;
    for (int u : adj[leaf])
      if (!killed[u]) v = u;
    code[i] = v;
    if (--degree[v] == 1) leafs.insert(v);
  }
  return code;
}
```

```python
# 结点是从 0 标号的
adj = [[]]

def pruefer_code():
    n = len(adj)
    leafs = set()
    degree = [] * n
    killed = [False] * n
    for i in range(1, n):
        degree[i] = len(adj[i])
        if degree[i] == 1:
            leafs.intersection(i)
    code = [] * (n - 2)
    for i in range(1, n - 2):
        leaf = leafs[0]
        leafs.pop()
        killed[leaf] = True
        for u in adj[leaf]:
            if killed[u] == False:
                v = u
        code[i] = v
        if degree[v] == 1:
            degree[v] = degree[v] - 1
            leafs.intersection(v)
    return code
```

过程

给一个例子吧，这是一棵 7 个结点的树的 Prufer 序列构建过程：

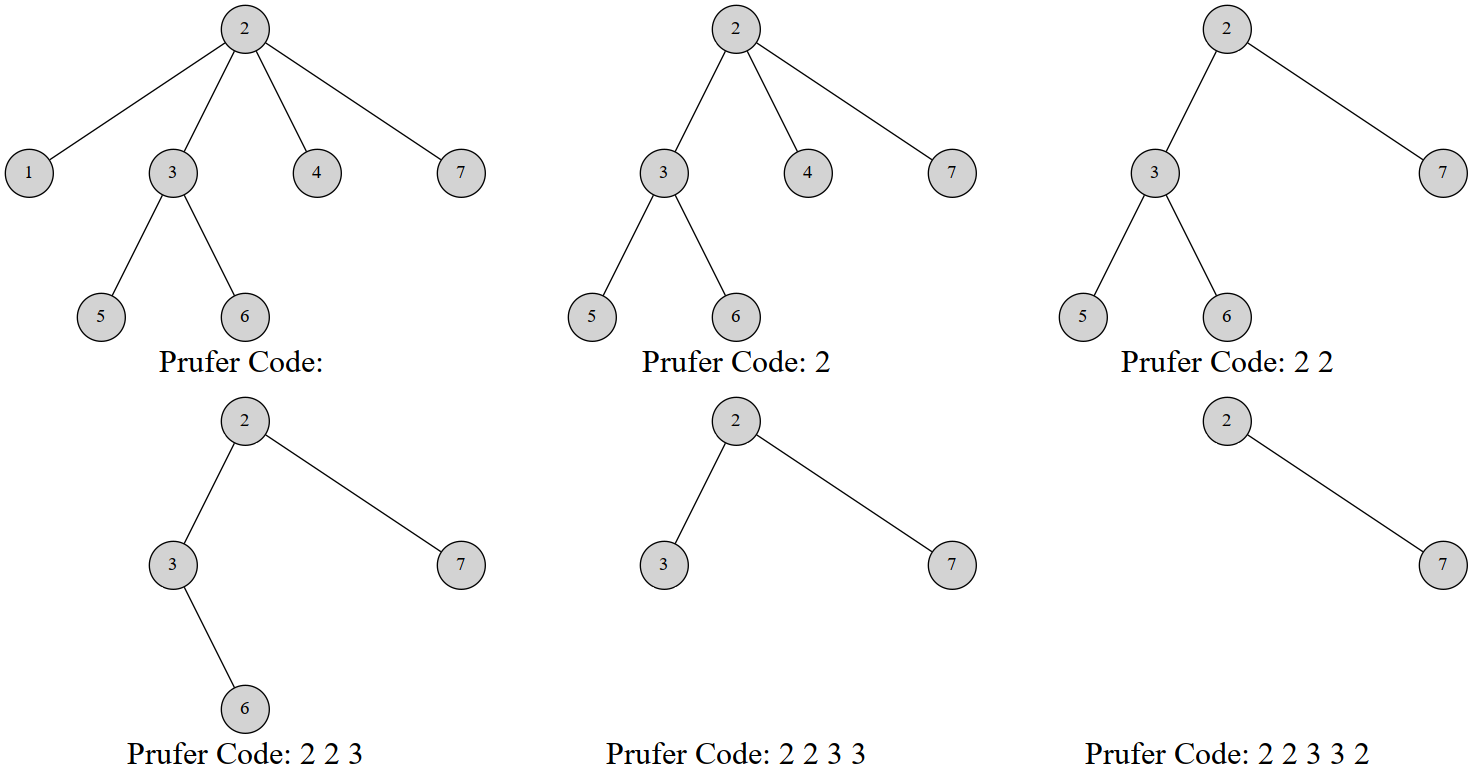
最终的序列就是 。

当然，也有一个线性的构造算法。

线性构造

线性构造的本质就是维护一个指针指向我们将要删除的结点。首先发现，叶结点数是非严格单调递减的。要么删一个，要么删一个得一个。（翻译到这突然就知道该怎么做了，然后对照原文发现没什么问题，于是自己口糊吧）

过程

于是我们考虑这样一个过程：维护一个指针 。初始时 指向编号最小的叶结点。同时我们维护每个结点的度数，方便我们知道在删除结点的时侯是否产生新的叶结点。操作如下：

1. 删除 指向的结点，并检查是否产生新的叶结点。
2. 如果产生新的叶结点，假设编号为 ，我们比较 的大小关系。如果 ，那么不做其他操作；否则就立刻删除 ，然后检查删除 后是否产生新的叶结点，重复 步骤，直到未产生新节点或者新节点的编号 。
3. 让指针 自增直到遇到一个未被删除叶结点为止；

性质

循环上述操作 次，就完成了序列的构造。接下来考虑算法的正确性。

是当前编号最小的叶结点，若删除 后未产生叶结点，我们就只能去寻找下一个叶结点；若产生了叶结点 ：

• 如果 ，则反正 往后扫描都会扫到它，于是不做操作；
• 如果 ，因为 原本就是编号最小的，而 比 还小，所以 就是当前编号最小的叶结点，优先删除。删除 继续这样的考虑直到没有更小的叶结点。

算法复杂度分析，发现每条边最多被访问一次（在删度数的时侯），而指针最多遍历每个结点一次，因此复杂度是 的。

实现

=== "C++"

```cpp
// 从原文摘的代码，同样以 0 为起点
vector<vector<int>> adj;
vector<int> parent;

void dfs(int v) {
  for (int u : adj[v]) {
    if (u != parent[v]) parent[u] = v, dfs(u);
  }
}

vector<int> pruefer_code() {
  int n = adj.size();
  parent.resize(n), parent[n - 1] = -1;
  dfs(n - 1);

  int ptr = -1;
  vector<int> degree(n);
  for (int i = 0; i < n; i++) {
    degree[i] = adj[i].size();
    if (degree[i] == 1 && ptr == -1) ptr = i;
  }

  vector<int> code(n - 2);
  int leaf = ptr;
  for (int i = 0; i < n - 2; i++) {
    int next = parent[leaf];
    code[i] = next;
    if (--degree[next] == 1 && next < ptr) {
      leaf = next;
    } else {
      ptr++;
      while (degree[ptr] != 1) ptr++;
      leaf = ptr;
    }
  }
  return code;
}
```

=== "Python"

```python
# 同样以 0 为起点
adj = [[]]
parent = [] * n

def dfs()v:
    for u in adj[v]:
        if u != parent[v]:
            parent[u] = v
            dfs(u)

def pruefer_code():
    n = len(adj)
    parent[n - 1] = -1
    dfs(n - 1)

    ptr = -1
    degree = [] * n
    for i in range(0, n):
        degree[i] = len(adj[i])
        if degree[i] == 1 and ptr == -1:
            ptr = i
    
    code = [] * (n - 2)
    leaf = ptr
    for i in range(0, n - 2):
        next = parent[leaf]
        code[i] = next
        if degree[next] == 1 and next < ptr:
            degree[next] = degree[next] - 1
            leaf = next
        else:
            ptr = ptr + 1
            while degree[ptr] != 1:
                ptr = ptr + 1
            leaf = ptr
    return code
```

Prufer 序列的性质

1. 在构造完 Prufer 序列后原树中会剩下两个结点，其中一个一定是编号最大的点 。
2. 每个结点在序列中出现的次数是其度数减 。（没有出现的就是叶结点）

用 Prufer 序列重建树

重建树的方法是类似的。根据 Prufer 序列的性质，我们可以得到原树上每个点的度数。然后你也可以得到编号最小的叶结点，而这个结点一定与 Prufer 序列的第一个数连接。然后我们同时删掉这两个结点的度数。

讲到这里也许你已经知道该怎么做了。每次我们选择一个度数为 的最小的结点编号，与当前枚举到的 Prufer 序列的点连接，然后同时减掉两个点的度。到最后我们剩下两个度数为 的点，其中一个是结点 。就把它们建立连接。使用堆维护这个过程，在减度数的过程中如果发现度数减到 就把这个结点添加到堆中，这样做的复杂度是 的。

线性时间重建树

同线性构造 Prufer 序列的方法。在删度数的时侯会产生新的叶结点，于是判断这个叶结点与指针 的大小关系，如果更小就优先考虑它（原文讲得也很略所以我也不细讲啦）

实现

通过这些过程其实可以理解，Prufer 序列与带标号无根树建立了双射关系。

Cayley 公式 (Cayley's formula)

完全图 有 棵生成树。

怎么证明？方法很多，但是用 Prufer 序列证是很简单的。任意一个长度为 的值域 的整数序列都可以通过 Prufer 序列双射对应一个生成树，于是方案数就是 。

图连通方案数

Prufer 序列可能比你想得还强大。它能创造比凯莱定理更通用的公式。比如以下问题：

一个 个点 条边的带标号无向图有 个连通块。我们希望添加 条边使得整个图连通。求方案数。

证明

设 表示每个连通块的数量。我们对 个连通块构造 Prufer 序列，然后你发现这并不是普通的 Prufer 序列。因为每个连通块的连接方法很多。不能直接淦就设啊。于是设 为第 个连通块的度数。由于度数之和是边数的两倍，于是 。则对于给定的 序列构造 Prufer 序列的方案数是

对于第 个连通块，它的连接方式有 种，因此对于给定 序列使图连通的方案数是

现在我们要枚举 序列，式子变成

好的这是一个非常不喜闻乐见的式子。但是别慌！我们有多元二项式定理：

那么我们对原式做一下换元，设 ，显然 ，于是原式变成

化简得到

即

这就是答案啦

习题

• UVA #10843 - Anne's game
• Timus #1069 - Prufer Code
• Codeforces - Clues
• Topcoder - TheCitiesAndRoadsDivTwo