Hamel基
前置知识:线性空间 的定义以及相关概念中的线性相关、线性无关、极大线性无关组、子空间等。
线性基是线性空间的一组基,是研究线性空间的重要工具。
Hamel 基
定义
称线性空间
规定线性空间
另外,将
- 若基是有限集合,则定义
- 若基不是有限集合,则定义
存在性
由 Zorn 引理,我们可以证明:任意线性空间均存在 Hamel 基。
证明思路如下:
设线性空间
容易验证
容易验证
性质(有限维)
-
对于有限维线性空间
-
-
-
若
任取
因此
-
-
-
(子空间维数公式)令
设
取
接下来只需证明向量组
设
则
注意到上式左边在
故
-
令
- 若
note1,3 两条可推广到无限维线性空间中
例子
考虑
-
如图
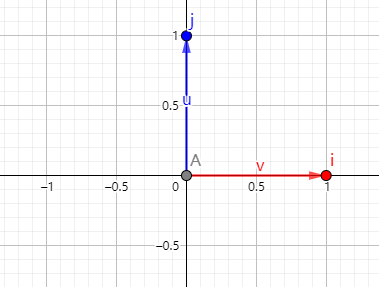
-
如图
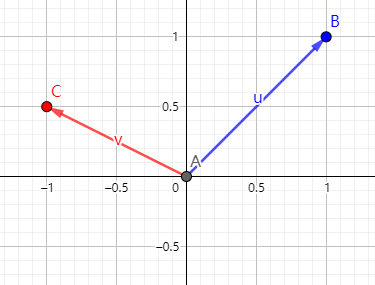
-
如图
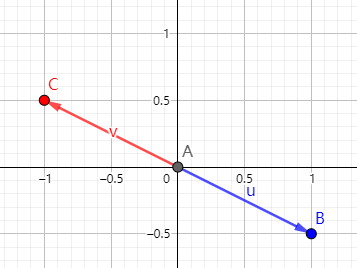
-
如图
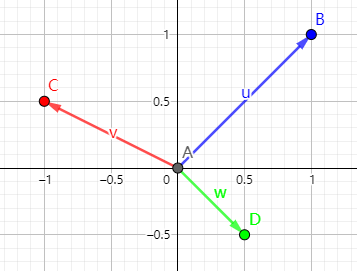
应用
线性基在 OI 中的应用一般包含以下方面:
- 对给定的向量组,找到一组极大线性无关组(或其张成的线性空间的一组基)。
- 向给定的向量组插入某些向量,在插入操作后的向量组中找到一组极大线性无关组(或其张成的线性空间的一组基)。
- 对找到的一组极大线性无关组(或基),判断某向量能否被其线性表出
- 求极大线性无关组(或基)的秩。
- 对找到的一组极大线性无关组(或基),求其张成的线性空间中的最大元/最小元。
特别地:
- 若限定向量均在
- 若限定向量均在
构造方法
因为异或线性基与实数线性基没有本质差别,所以接下来以异或线性基为例,实数线性基版本的代码只需做一点简单修改即可。
贪心法
对原集合的每个数
查询原集合内任意几个元素
为什么能行呢?因为从高往低位扫,若当前扫到第
查询原集合内任意几个元素
查询某个数是否能被异或出来,类似于插入,如果最后插入的数
高斯消元法
高斯消元法相当于从线性方程组的角度去构造线性基,正确性显然。
性质
贪心法构造的线性基具有如下性质:
- 线性基没有异或和为
- 线性基中各数二进制最高位不同。
高斯消元法构造出的线性基满足如下性质:
-
高斯消元后的矩阵是一个行简化阶梯形矩阵。
该性质包含了贪心法构造的线性基满足的两条性质
如果不理解这条性质的正确性,可以跳转 高斯消元。
提供一组样例:
5
633 211 169 841 1008二进制表示:
1001111001
0011010011
0010101001
1101001001
1111110000贪心法生成的线性基:
1001111001
0100110000
0011010011
0001111010
0000000000
0000010000
0000000000
0000000000
0000000000
0000000000高斯消元法生成的线性基:
1000000011
0100100000
0010101001
0001101010
0000010000
0000000000
0000000000
0000000000
0000000000
0000000000这是一条非常好的性质,能帮我们更方便的解决很多问题。比如:给定一些数,选其中一些异或起来,求异或最大值,如果用贪心法构造线性基,需要再做一遍贪心,如果 ans 的当前位是 0,那么异或一定会更优,否则当前位如果为 1,则一定不会更优;而使用高斯消元法构造线性基后直接将线性基中所有元素都异或起来输出即可。
对于其他比较经典的问题(查询一个数能否被异或得到,查询能被异或得到的第
时间复杂度
设向量长度为
若是实数线性基,则时间复杂度为
练习题
- Luogu P3812【模板】线性基
- Acwing 3164. 线性基
- SGU 275 to xor or not xor
- HDU 3949 XOR
- HDU 6579 Operation
- Luogu P4151[WC2011]最大 XOR 和路径
参考资料与注释
- 丘维声,高等代数(下)。清华大学出版社。
- Hamel Basis -- from Wolfram MathWorld
贡献者:@queenwen@Tifa@WenzelTian@Great-designer
本页面最近更新:2/3/2023, 12:00:00 AM,更新历史
发现错误?想一起完善? 在 GitHub 上编辑此页!
本页面的全部内容在 CC BY-SA 4.0 和 SATA 协议之条款下提供,附加条款亦可能应用