图的着色
点着色
(讨论的是无自环无向图)
对无向图顶点着色,且相邻顶点不能同色。若 G 是
对任意图 G,有
Brooks 定理
设连通图不是完全图也不是奇圈,则
证明
设
首先,
接下来,假设对于
不妨只考虑
对于任意不是完全图也不是奇圈的正则图 G,任取其中一点 v,考虑子图
令
接下来我们设所有在 H 中染成
这里的交换颜色指的是若图中只有两种颜色 a,b,那么把图中原来染成颜色 a 的点全部染成颜色 b,把图中原来染成颜色 b 的点全部染成颜色 a。
我们设上述连通分量为
然后我们不难发现,对任意 3 个不同的点
到这里我们对命题的强化工作就已经做完了。
接下来就很简单。首先,如果 v 的邻接点两两相邻,那么命题得证。不妨设
至此命题证明完毕。
Welsh—Powell 算法
Welsh—Powell 算法是一种在 不限制最大着色数 时寻找着色方案的贪心算法。
对于无自环无向图 G,设
按 Welsh—Powell 算法着色后的颜色数至多为
过程
- 将当前未着色的点按度数降序排列。
- 将第一个点染成一个未被使用的颜色。
- 顺次遍历接下来的点,若当前点和所有与第一个点颜色 相同 的点 不相邻,则将该点染成与第一个点相同的颜色。
- 若仍有未着色的点,则回到步骤 1, 否则结束。
示例如下:
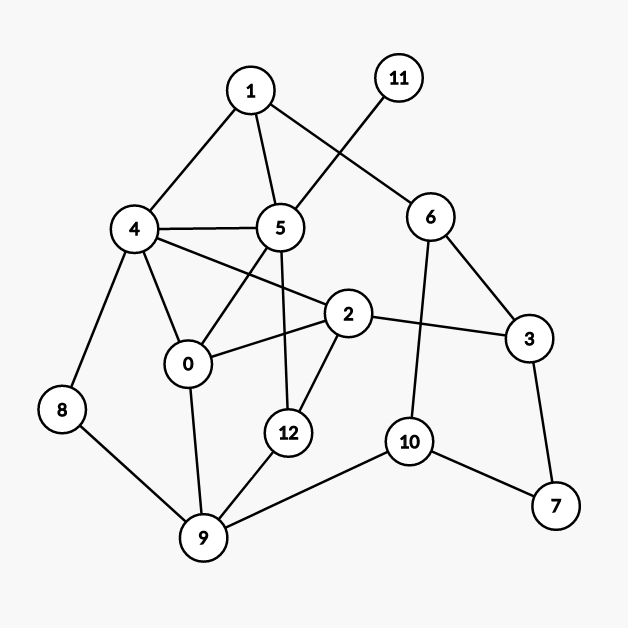
(由 Graph Editor 生成)
我们先对点按度数降序排序,得:
| 次序 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 点的编号 | 4 | 5 | 0 | 2 | 9 | 1 | 3 | 6 | 10 | 12 | 7 | 8 | 11 |
| 度数 | 5 | 5 | 4 | 4 | 4 | 3 | 3 | 3 | 3 | 3 | 2 | 2 | 1 |
| 1 | 2 | 3 | 4 | 5 | 4 | 4 | 4 | 4 | 4 | 3 | 3 | 2 |
所以 Welsh—Powell 算法着色后的颜色数最多为 5。
另外因为该图有子图
-
第一次染色:
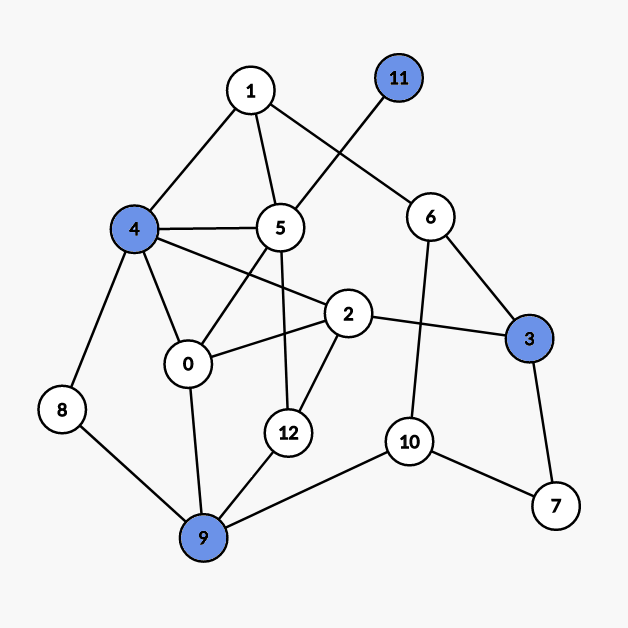
染
4 9 3 11号点。 -
第二次染色:
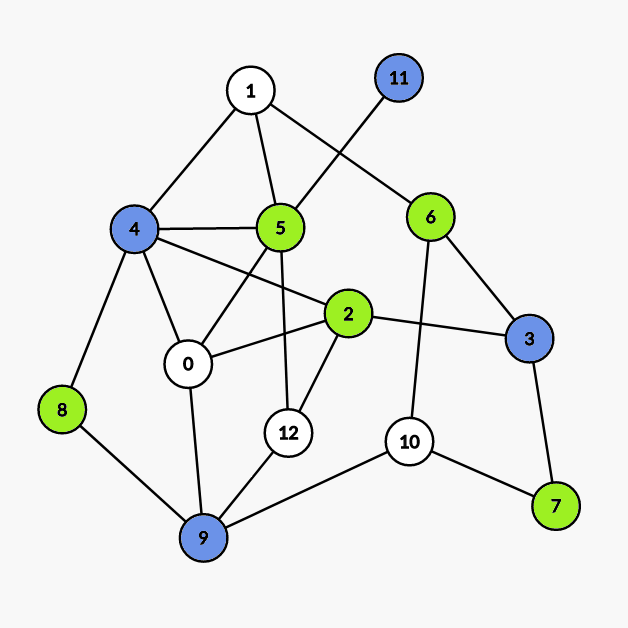
染
5 2 6 7 8号点。 -
第三次染色:
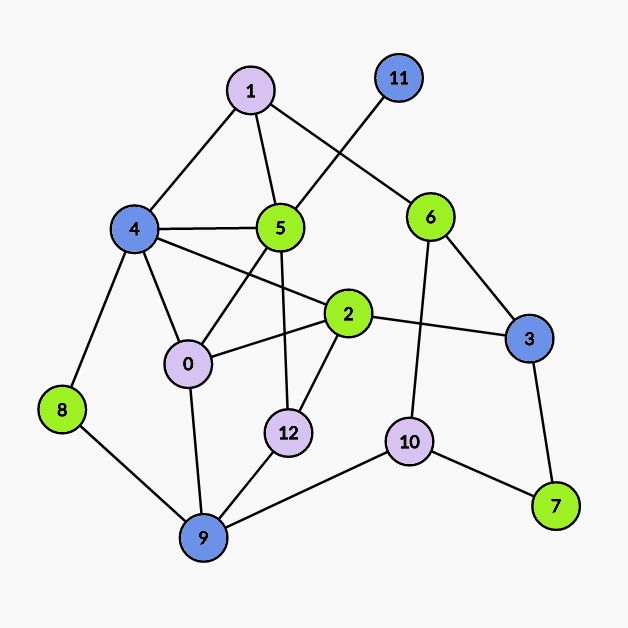
染
0 1 10 12号点。
证明
对于无自环无向图 G,设
令
-
-
若
则
-
-
-
显然若将
我们只需要证明:
其中
上式左边的不等号显然成立,我们考虑右边。
首先我们不难得出:
若
进而
另一方面,基于序列
两式结合即得证。
边着色
对无向图的边着色,要求相邻的边涂不同种颜色。若 G 是 k- 边可着色的,但不是
Vizing 定理
设 G 是简单图,则
若 G 是二部图,则
当
二分图 Vizing 定理的构造性证明
按照顺序在二分图中加边。
我们在尝试加入边
如果
否则假设
修改的过程可以被近似的看成是一条从
因为增广路有限所以我们可以将增广路上所有的边反色,即原来颜色为
根据二分图的性质,节点
所以我们可以在增广之后直接将连接
总构造时间复杂度为
本题为笔者于 2018 年命制的集训队第一轮作业题。
首先我们可以发现答案下界为度数不为 k 倍数的点的个数。
下界的构造方法是对二分图进行拆点。
若
若
拆出来的点在原图中的意义相同,也就是说,在满足度数限制的情况下,一条边端点可以连接任意一个拆出来的点。
根据 Vizing 定理,我们显然可以构造出该图的一种 k 染色方案。
删边部分由于和 Vizing 定理关系不大这里不再展开。
有兴趣的读者可以自行阅读笔者当时写的题解。
色多项式
在无向无环图 G 中,
定理:设
其中
参考资料
- Graph coloring - Wikipedia
- Welsh, D. J. A.; Powell, M. B. (1967), "An upper bound for the chromatic number of a graph and its application to timetabling problems", The Computer Journal, 10 (1): 85–86
贡献者:@Imple@WenzelTian@Tifa@CoderOJ@mgt@Chrogeek@zhouyuyang2002@Ir1d
本页面最近更新:2/3/2023, 12:00:00 AM,更新历史
发现错误?想一起完善? 在 GitHub 上编辑此页!
本页面的全部内容在 CC BY-SA 4.0 和 SATA 协议之条款下提供,附加条款亦可能应用